相信大家對Fibonacci這個名稱應該都不陌生
就直接來看題目的定義吧!

Given n, calculate F(n).

F(0) = 0, F(1) = 1
F(n) = F(n - 1) + F(n - 2), for n > 1.

fibonacci可以說是認識遞迴最好的題目

看到題目最直覺的想法如下

if n =1:
    return 0;

if n =2:
    return 1;

else:
    return fib(n-1) + fib(n-2)

直接轉換成javascript應該就如下

  function fib(n) {
    if (n === 1) {
      return 0;
    } else if (n === 2) {
      return 1;
    } else {
      return fib(n - 1) + fib(n - 2);
    }
  }

但這種方式我們其實會重複做很多的事

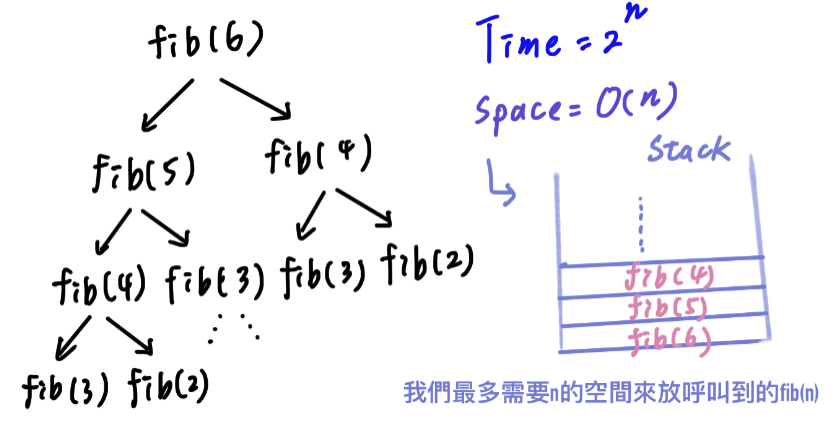
從這張圖可以看到
我們在fib(5)呼叫了fib(4)
再計算fib(6)時又會去呼叫fib(4)
當n很大時，重複計算是很耗費時間的！

這時候我們就應該思考
『有辦法減少重複做的事？』
如果我們把已經算好的數都存到hashTable這樣我們就可以以 O(1) 的時間取得我們要的值

就像是查表一樣(有一點Dynamic Programming （DP）的感覺 -> 明天會介紹)
因此，我們可以讓時間複雜度降低到 O(n)
而空間複雜度，我們最多儲存n個數在我們要查的表中，所以space一樣是 O(n)

  function fib(n, table = { 1: 0, 2: 1 }) {
    if (n in table) {
      return table[n];
    } else {
      table[n] = fib(n - 1, table) + fib(n - 2, table);
      return table[n];
    }
  }

既然我們可以降低時間複雜度
我們接著思考
『有沒有辦法再降低空間複雜度?』

我們真的有需要把所有fib(n)的計算結果都存起來嗎？
當我們要算fib(3)其實只需要fib(2)和fib(1)

每一次計算其實都只用前兩個的結果
也就是我們只需要去存當下要算的前面兩個結果
而用不到的就丟到垃圾桶，對吧？
結論-> 我們可以用一個長度為2的陣列來儲存前面兩個結果就好！
來看看實際的做法吧！

Time: O(n)，Space: O(1)

var fib = function(n) {
    if (n === 0) return 0;
    if (n === 1) return 1;
    //迷你庫存
    const lastTwo = [1, 1];
    let count = 3;
    while (count <= n) {
    //更新庫存
      const nextFib = lastTwo[0] + lastTwo[1];
      lastTwo[0] = lastTwo[1];
      lastTwo[1] = nextFib;
      count++;
    }
    return lastTwo[1];
  };

看完這些方式，也別忘記自己實做看看喔！
唯有自己Coding過才會知道自己的bug在哪邊！用看的感覺和做起來差很大！！

明日題目預告:
小時候很常被問到的湊錢問題：Coin Change